笛卡儿，法国著名哲学家、数学家、物理学家，他的著名哲学观点“我思故我在”常被人们称道。笛卡儿堪称17世纪的欧洲哲学界和科学界最有影响的巨匠之一，被誉为“近代科学的始祖”。笛卡尔的著作，无论是数学、自然科学，还是哲学，都开创了这些学科的崭新时代。尤其是对数学的贡献功不可没，笛卡尔认为，“科学的本质是数学”.

在笛卡儿之前，几何与代数是数学中两个截然不同的研究领域。笛卡儿站在方法论的自然哲学的高度，认为希腊人的几何学过于依赖于图形，束缚了人的想象力。笛卡儿的核心思想是：把几何学的问题归结成代数形式的问题，用代数学的方法进行计算、证明，从而达到最终解决几何问题的目的。依照这种思想，他发表了著作《几何学》，创立了直角坐标系，从而打开了近代数学的大门。

该著作虽然只有117页，但它标志着代数与几何的第一次完美结合，它把相互对立的“数”与“形”统一了起来，使形形色色的代数方程表现为不同的几何图形，许多相当难解的几何问题转化为代数问题后，便能轻而易举地得到解决.笛卡儿的这一天才创见，在科学史上具有划时代的意义，它为牛顿和莱布尼茨发现微积分奠定了基础。

同牛顿、莱布尼茨一样，笛卡尔终生未婚.他死后，坟墓曾遭到盗墓贼挖掘.1799年法国大革命后，笛卡尔的骨灰和遗物被送进法国历史博物馆。1819年，其骨灰被移入巴黎圣心堂，人们在他的墓碑上刻下了这样一句话：“笛卡尔，欧洲文艺复兴以来，第一个为人类争取并保证理性权利的人。”他的哲学与数学思想对历史的影响是很深远的。

关于直角坐标系的由来，传说有这么一个故事：

有一天，笛卡尔生病卧床，但他头脑一直没有休息，在反复思考一个问题：几何图形是直观的，而代数方程比较抽象，能不能用几何图形来表示代数方程呢？这里，关键是如何把组成几何图形的点和满足方程的每一组“数”挂上钩.他就拼命琢磨.通过什么样的办法才能把“点”和“数”联系起来呢？突然，他看见屋顶角上的一只蜘蛛，拉着丝垂了下来，一会儿，蜘蛛又顺着丝爬上去，在上边左右拉丝.蜘蛛的“表演”，使笛卡尔思路豁然开朗.他想，可以把蜘蛛看做一个点，它在屋子里可以上、下、左、右运动，能不能把蜘蛛的每个位置用一组数确定下来呢？他又想，屋子里相邻的两面墙与地面交出了三条线，如果把地面上的墙角作为起点，把交出来的三条线作为三根数轴，那么空间中任意一点的位置，不是可以用这三根数轴上对应顺序的三个数来表示吗？反过来，任意给出一组三个有顺序的数，例如3、2、1，也可以用空间中的一个点P来表示它们（如图1）.同样，用一组数（a，b）可以表示平面上的一个点，平面上的一个点也可以用一组两个有顺序的数来表示（如图2）.于是在蜘蛛的启示下，笛卡尔创建了直角坐标系.

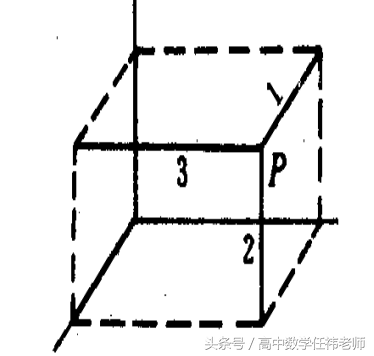
图一

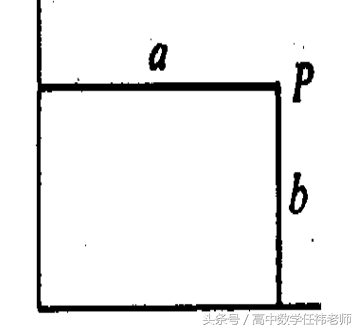
图二

无论这个传说的可靠性如何，有一点是可以肯定的，就是笛卡尔是个勤于思考的人.他在创建直角坐标系的过程中，很可能是受到周围一些事物的启发，触发了灵感.