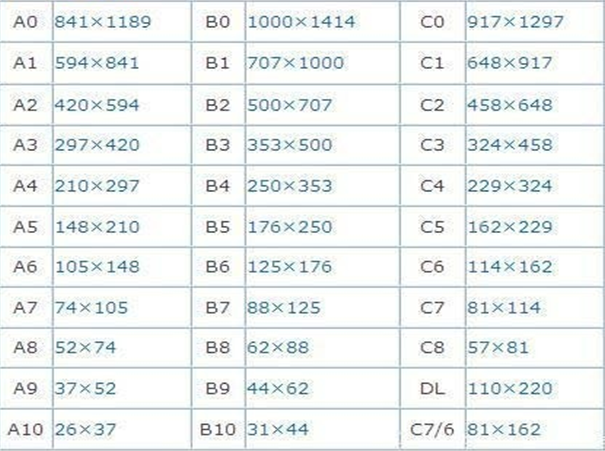
上图概括了几乎所有标准图纸大小,但具体为什么这么定义你知道吗?
可以运算一下,上面这些纸张的长宽之比都符合多少?对,√2,国际规定纸张的幅宽(以X表示)和长 度(以Y表示)的比例关系为X:Y=1:1.414(即√2),为什么是这个呢?你可以想象一个等腰直角三角形,当你沿中线对折后,就会发现出来的仍旧是等腰直角三角形,与原三角形相似,面积减半。对,细想等腰直角三角形斜边和直角边之比是不是也是√2?,这√2是何方神圣?哈哈,数学上定义√2为“白银比例”,是不是比较熟悉,对,就和“黄金比例”(0.618)是同胞兄弟。那为什么纸的比例不按最美比例0.618走呢?因为人们应用中,难免对纸进行折叠,这就需要折出来的大小应和原比例类似,这样打印也方便,只要成比例放大缩小即可。这就是白银比例的最好体现。
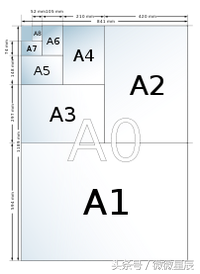
那为什么分A0\A1\A2\B1等等呢?为什么我A4尺寸要定义为210*297呢?我们先看A0和后续A1怎么定义的,定义为A0纸折叠一次大小就是A1,两次就是A2,n次就是An了。同时为了方便,就定义初始尺寸A0(841*1189)面积为1平方米,这样更方便裁剪。因此便有了后续一系列大小。
但有时我们在应用时候,A系列的纸大小并不一定符合我们使用大小,可能A3大,A4小,这是就选取了中间大小,定义了B系列纸张。B系列纸张的大小由编号相同与编号少一号的A组纸张的几何平均决定的,比如:B1是A1 和A0的几何平均。同理, C组纸张尺寸是编号相同的A、B组纸张的几何平均,例如:C2是B2和A2的几何平均。B组纸张用途并非刚好符合使用大小那么简单,我们文件收藏时,不能A4纸就用A4大小的纸盒,这样是装不进去的,所以这时就可以用B4大小的文件夹收藏A4大小的文件啦。
C组纸张尺寸主要使用于信封。一张A4大小的纸张可以刚好放进一个C4大小的信封。 如果你把A4纸张对折变成A5纸张,那它就可以刚好放进C5大小的信封,同理类推。
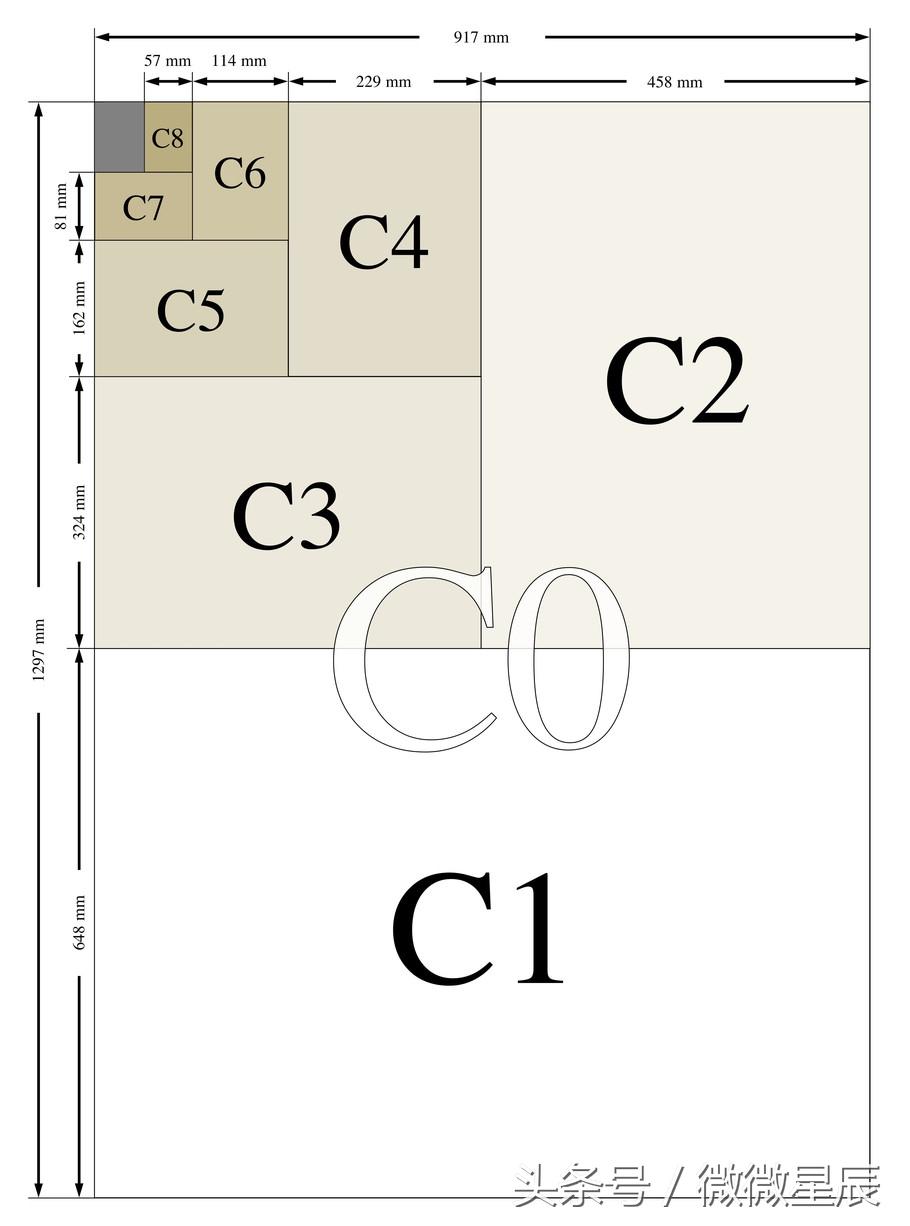
同时图中还有两个特殊尺寸,DL和C7/6,这两个长宽比是特殊定义的为2。比如我们的信封都是这种大小,这样基本上是符合了我们大多用纸需求啦。

