区间
区间是高等数学课程中用得较多的一类数集.
设a和b都是实数,且a<b,数集{x|a<x<b}称为开区间,记作(a,b)
即(a,b)={x|a<x<b}
a和b称为开区间(a,b)的端点,其中a为左端点,b为右端点,且a∉(a,b),b∉(a,b)

数集{x|a≤x≤b}称为闭区间,记作[a,b] 即[a,b]={x|a≤x≤b}
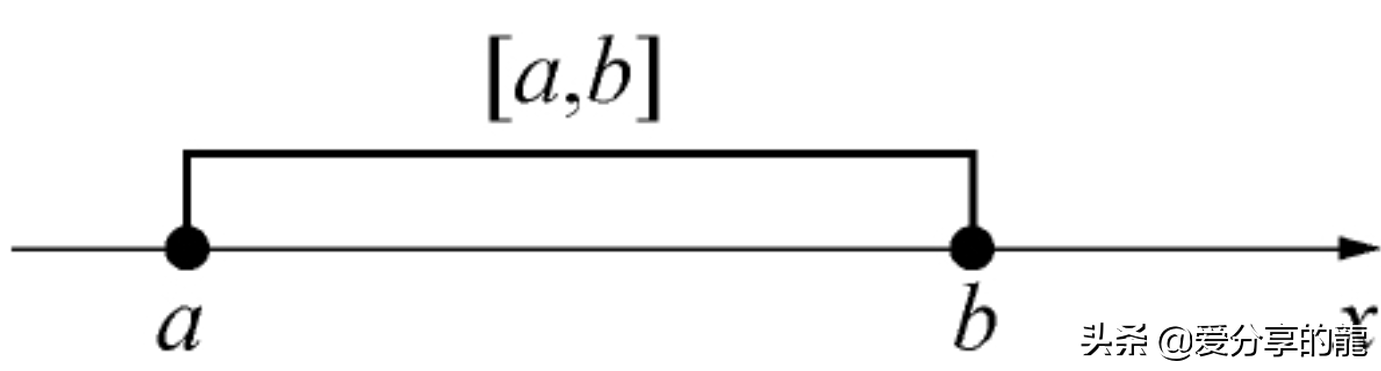
a和b也称为闭区间[a,b]的端点,且a∈[a,b],b∈[a,b]
数集{x|a≤x<b}及{x|a<x≤b}称为半开区间 分别记作[a,b)和(a,b]
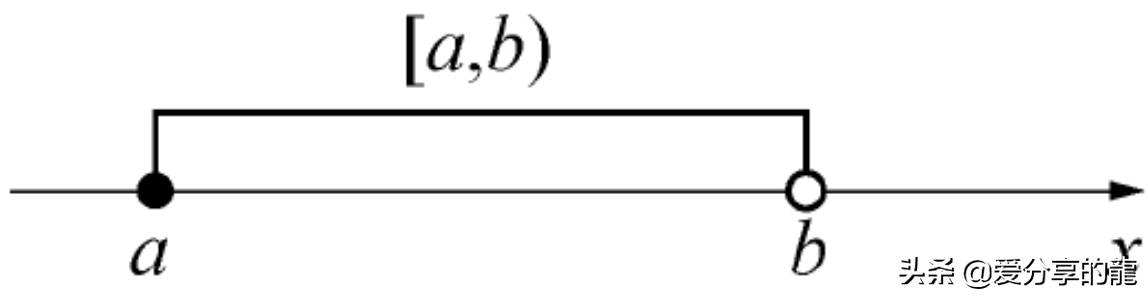
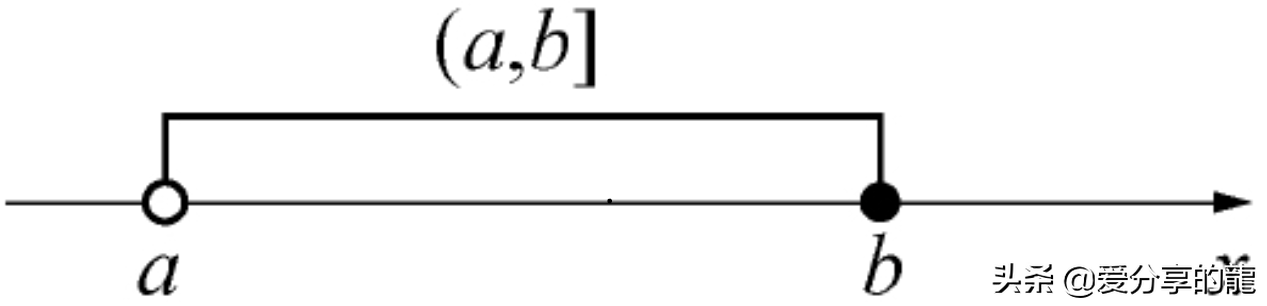
以上这些区间都称为有限区间,数b-a称为这些区间的长度.从数轴上看,这些区间是长度为有限的线段.
对于这样的集合:{x|x≥a},{x|x>a},{x|x≤b},{x|x<b},我们引进记号+∞(读作正无穷大)及-∞(读作负无穷大),则可用类似于有限区间的记号来表示无限的半开区间或开区间
[a,+∞)={x|x≥a}
(a,+∞)={x|x>a}
(-∞,b]={x|x≤b}
(-∞,b)={x|x<b}.这些区间在数轴上表示长度无限的半直线

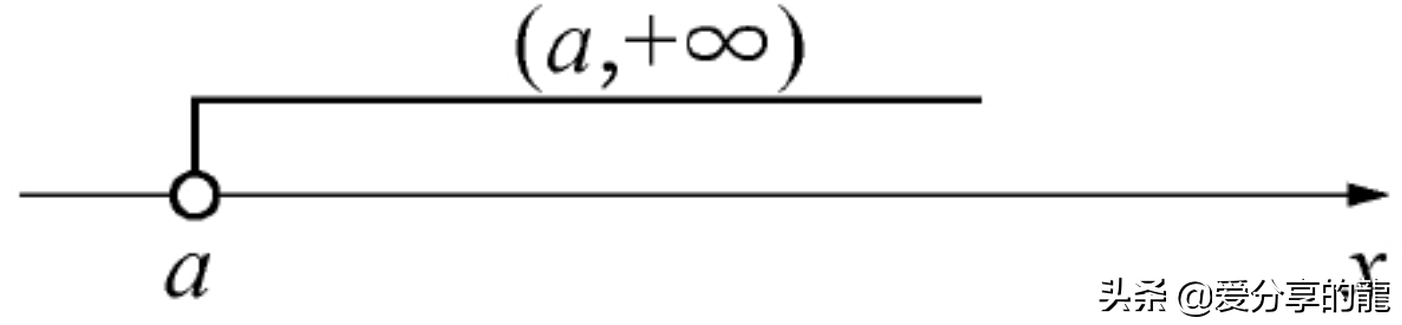
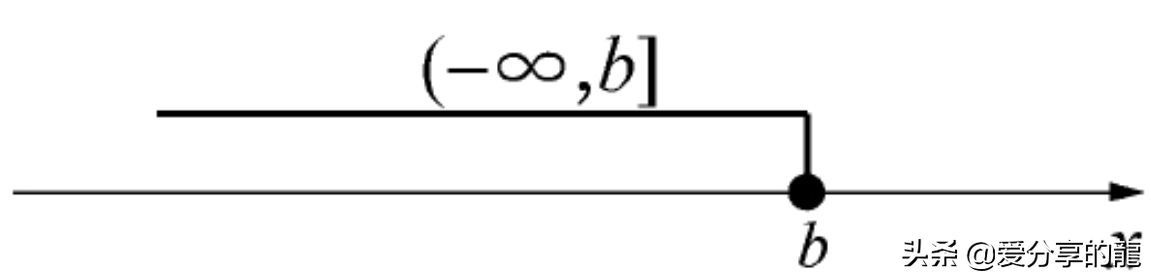
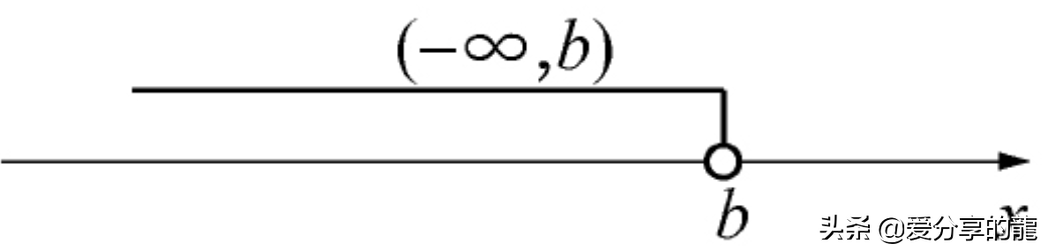
全体实数的集合R也记作(-∞,+∞),它也是无限的开区间.以后如果不需要辩明所讨论的区间是开区间还是闭区间,是有限区间还是无限区间,我们就简单地称其为区间,用 “I”代表各种类型的区间.
邻域
设a与δ为两个实数,且δ>0,数集{x||x-a|<δ}称为点a的δ邻域 记作U(a,δ)
即U(a,δ)={x||x-a|<δ},其中a称作U(a,δ)的中心,δ称作U(a,δ)的半径
在数轴上,|x-a|表示点x与点a的距离
因此点a的δ邻域U(a,δ)={x||x-a|<δ}在数轴上就表示与点a的距离小于δ的点x的全体
由于|x-a|<δ等价于-δ<x-a<δ,即a-δ<x<a+δ
所以U(a,δ)={x|a-δ<x<a+δ}
因此,U(a,δ)也就是开区间(a-δ,a+δ)这个开区间以点a为中心,长度为2δ

有时用到的邻域需要将邻域中心去掉 点a的δ邻域去掉中心a后,称为点a的去心δ邻域 记作



这里,0<|x-a|就表示x≠a.为了方便,有时将开区间(a-δ,a)称为a的左邻域,而将开区间(a,a+δ)称为a的右邻域.如果不强调半径,以点a为中心的任何开区间称为点a的邻域,记作U(a)

