求二面角是高考数学的热点问题,几乎在每一年高考数学中都有涉及到求解二面角。只要我们掌握了以下四种经典求法,基本就能应对所有的求解二面角的问题。
1、定义法:过二面角棱上任一点,在两个面内分别作垂直于棱的直线,则两直线所构成的角即为所求二面角的平面角。

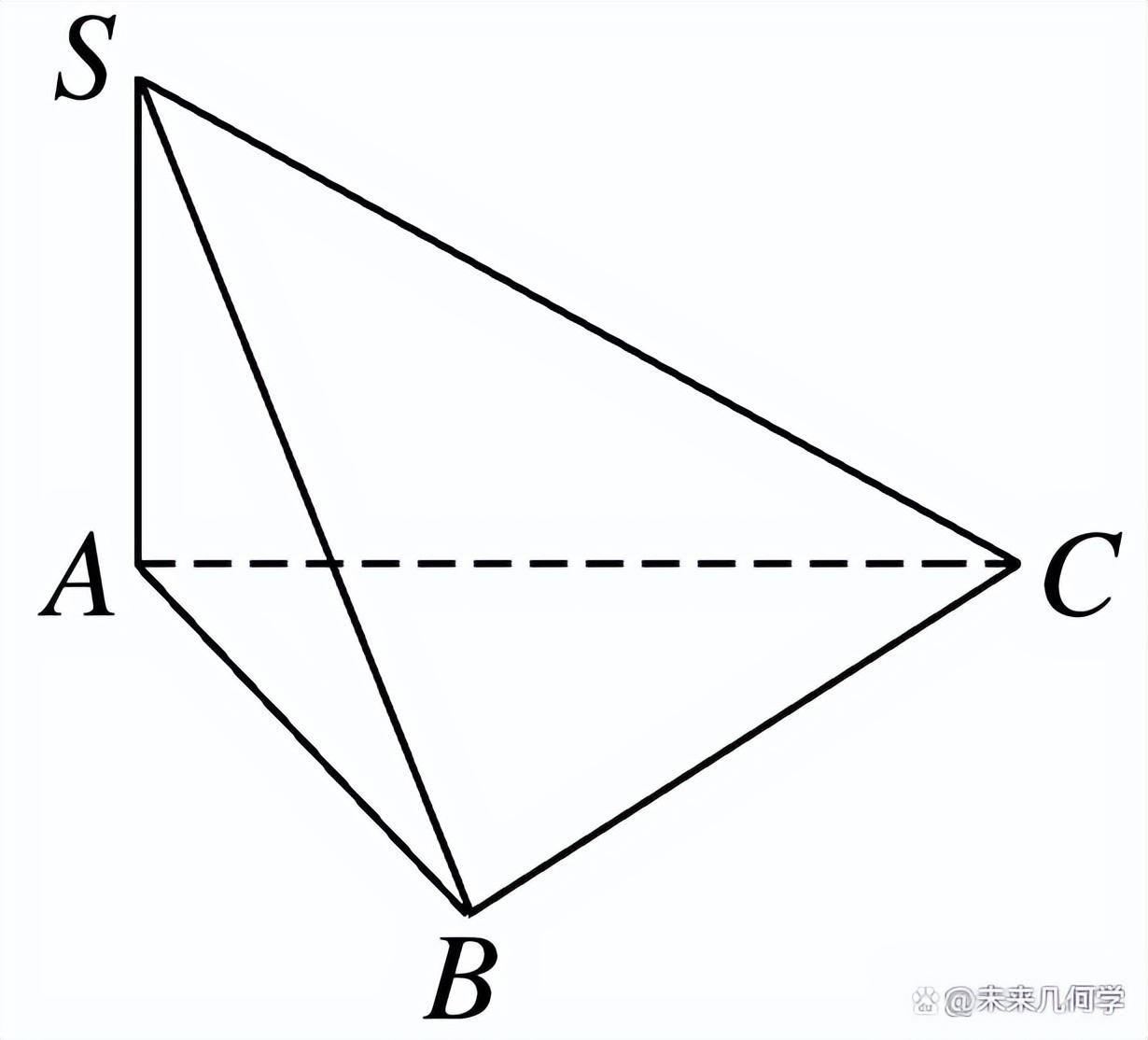
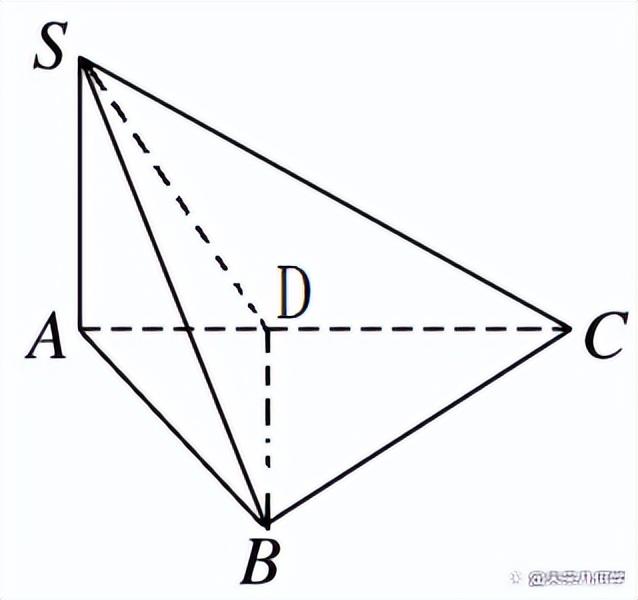
例1、如图,在三棱锥S-ABC中,∠SAB=∠SAC=∠ABC=90°,SA=AB,SB=BC.
(1)证明:平面SBC⊥平面SAB;
(2)求二面角A-SC-B的平面角的正弦值.

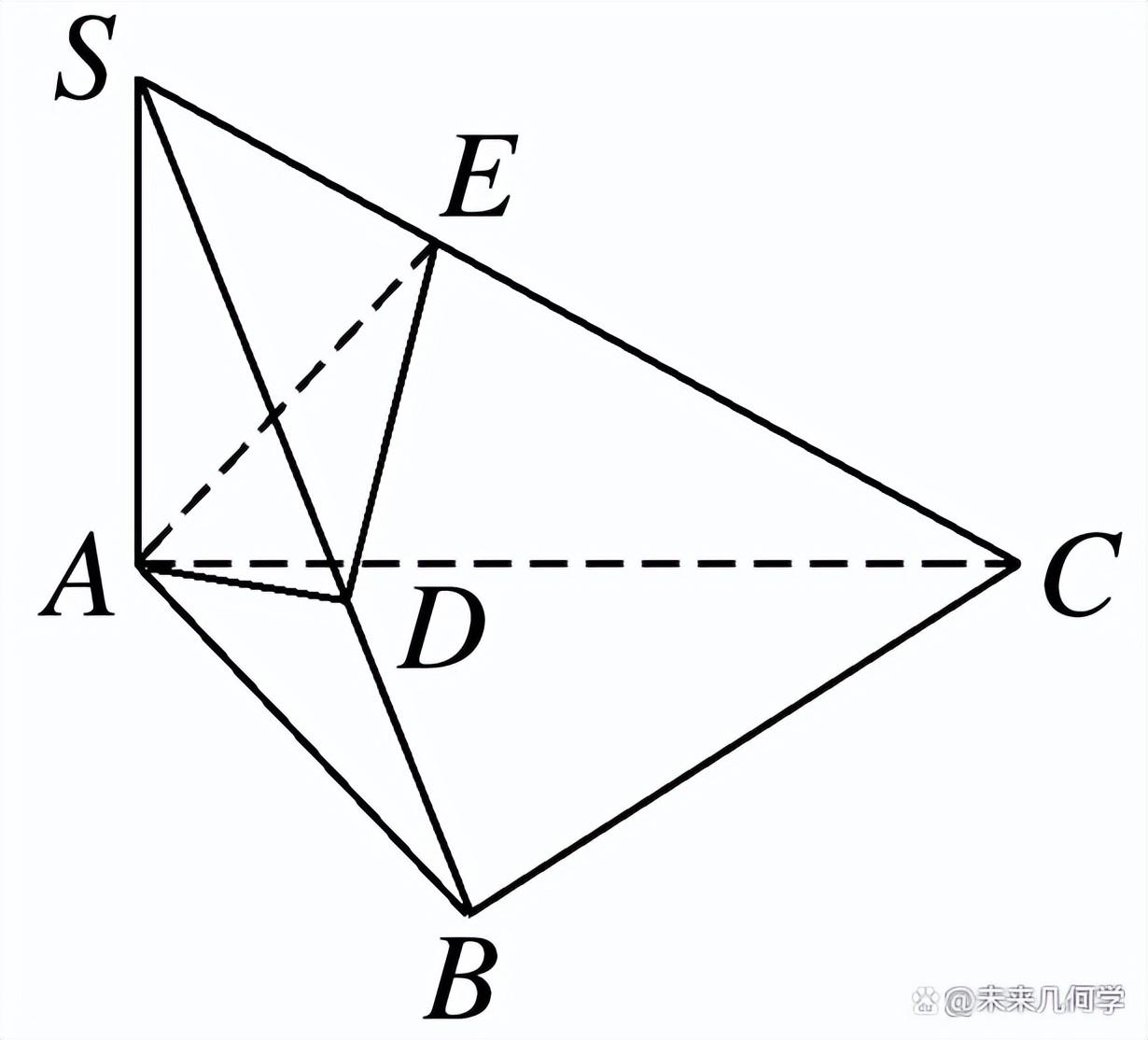
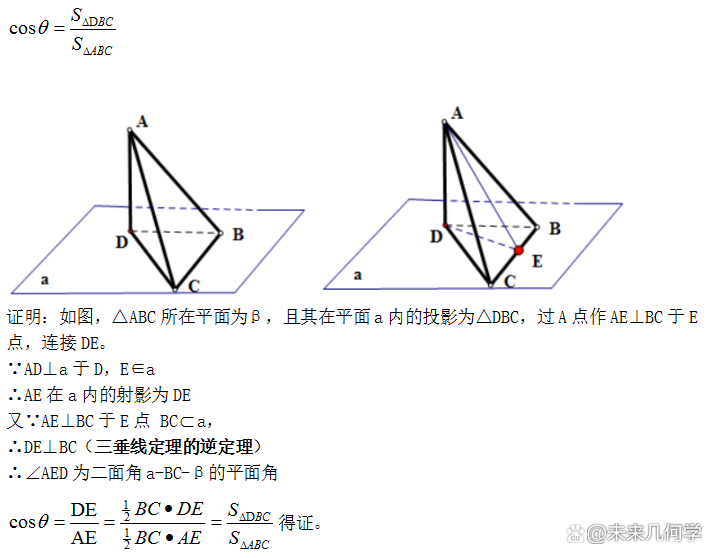
二、射影面积求二面角
平面ABC与平面a所成二面角为θ,它在平面a内的投影为DBC,则平面ABC与平面a所成二面角的余弦值为射影面积与原面积的比:

3、三垂线法
三垂线定理指的是平面内的一条直线,如果与穿过这个平面的一条斜线在这个平面上的射影垂直,那么它也与这条斜线垂直。
根据三垂线定理的思想构造出二面角的平面角,继而求出二面角的平面角的方法。
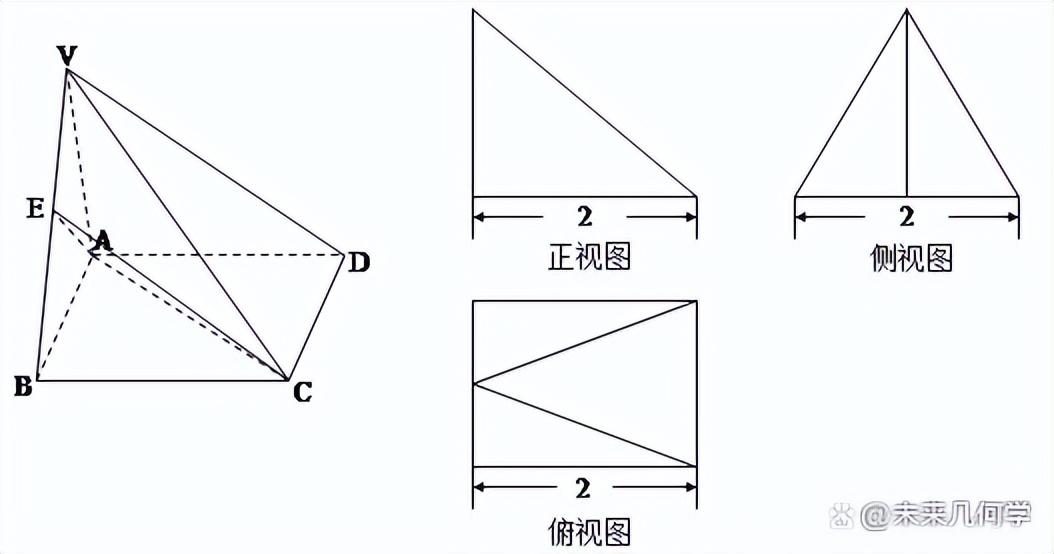
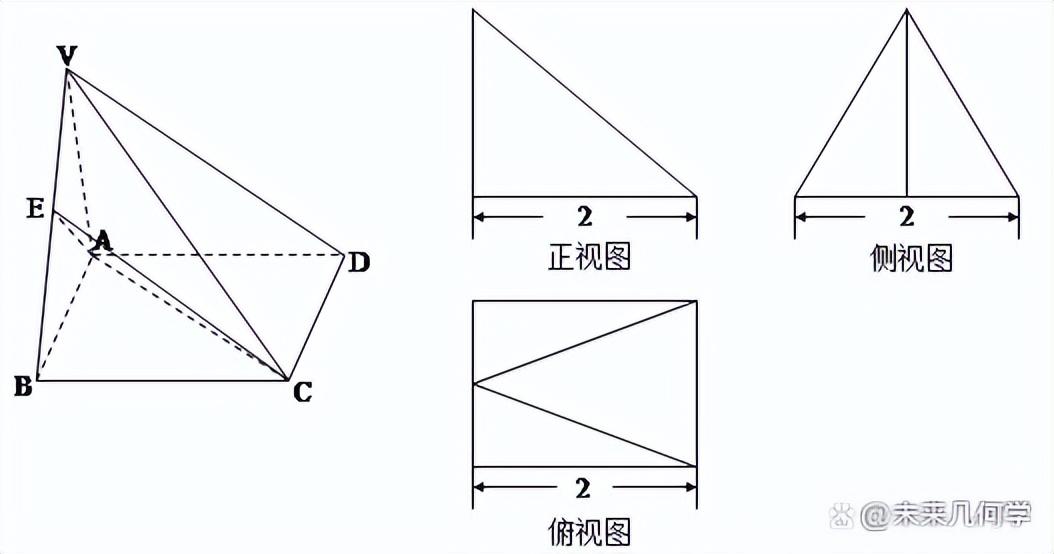
例3、如图所示的多面体,它的正视图为直角三角形,俯视图为正三角形,俯视图为正方形(尺寸如图所示),E为VB的中点。
(1)求证:VD∥平面EAC;
(2)求二面角A-VB-D的余弦值。

四、法向量法
适用于容易建立直角坐标系的题目。先求出与二面角的两个面垂直的两个向量所成的角,利用此角与二面角的平面角相等或互补的关系,求出二面角。
例4、同例3第(2)问
如图所示的多面体,它的正视图为直角三角形,俯视图为正三角形,俯视图为正方形(尺寸如图所示),E为VB的中点。
求二面角A-VB-D的余弦值。